|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Examples: Absorption Costing & Marginal CostingQ. Rajkumar Ltd. provides you the following information
You are required to calculate:
i)
ii) Fixed Cost = Contribution - Profit
iii)
= 5000 iv)
= 12500 v) Profit = Sales - Variable cost - Fixed cost Q. From the following information relating to Smith sons, calculate the break-even point and the turnover required to earn a profit of Rs. 3,00,000Fixed Overhead = 2,10,000 (total)
Calculation of turnover to earn a profit of Rs. 3,00,000
= 17000 units
= 8,50,000 Margin of Safety Margin of safety = Total sales - sales at BEP > For theory part please refer to chapter 9. Q. Premier Ltd. produces a standard article. The results of the last four quarters of the year 2000 are as follows:
The cost of direct material is Rs. 30 and direct labour is Rs. 20 per unit. Variable expenses are Rs 10 per unit. Fixed expenses are Rs 6,000 per annum. (i) Find out full cost percent for each quarter. (ii) Find out BEP (Break Even Point) in units for each quarter if selling price is Rs 100 per unit and the entire output is sold.
Annual expenses = 6000 i) Full cost percent for each quarter
ii) BEP in units BEP = Fixed cost/ contribution per unit Contribution = Sales - Variable cost BEP = 6000/40 = 150 units Q. From the following data :Selling Price = Rs. 40 per unit Calculate : i) Break-even point expressed in rupee sales. ii) Number of units that must be sold to earn a profit of Rs. 2,00,000 per year.
i) Contribution = Sales - variable cost Total fixed cost = Fixed factory overheads + Fixed selling cost
= 1,40,000 units BEP (Value) = Fixed cost/(P/V ratio)
= 10/40 X 100 = 25% BEP (value) = (14,00,000/25) X 100 ii) Number of units must be sold to earn a profit of Rs. 2,00,000 per year
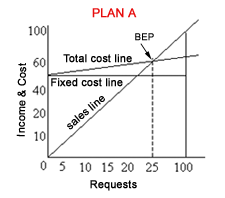
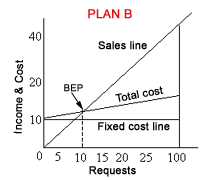
= (14,00,000 + 2,00,000) / 25% Q. A medical advisory service offers to its subscribers
complete information on doctors, paramedicals, health insurance,
super speciality hospitals and general health awareness. It now
plans to computerise these sevices and has a choice of two systems
on which to offer these services. Under option A, a computer system
would be leased for Rs. 50 lakhs per year and the subscriber requests
would be processed with avariable cost of Rs. 20 per request. Under
plan B, a computer system would be leased for Rs. 10 lakhs per year
and the subscriber requests would be processed with a variable cost
of Rs. 120 per request. Under either option, the subscriber can
and is happy to pay Rs 220 per request that is processed. On the
basis of this data
PLAN A BEP (units) = Fixed costs/contribution per unit PLAN B BEP (units) = Fixed costs/contribution per unit Plan is more risky because initial fixed cost is very high. If sales fall below 25,000 requests, losses will be incurred. (ii) Break even chart
iii) Profit under plan A = (Price - Varaible cost) X Units
- FC Profit under plan B = (220 - 120) X (x) - 10,00,000 Equating both the equations we get (220 - 20) X (x) - 50,00,000 = (220 - 120) X (x) - 10,00,000 iv) Operating Leverage Degree of operating leverage = %change in net operating income
/ % change in units sold or sales Where EBIT is Earning before interest & tax In both the plans the contribution is calculated taking hypothetical data of 50,000 requests because the question does not provide any information. PLAN A
= 2 PLAN B
= 1.25 Plan A has greater operating leverage owing to higher fixed costs. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |