Two Phase Method: Linear Programming
In Two Phase Method, the whole procedure of solving a linear programming problem (LPP) involving artificial variables is divided into two phases.
In phase I, we form a new objective function by assigning zero to every original variable (including slack and surplus variables) and -1 to each of the artificial variables. Then we try to eliminate the artificial varibles from the basis. The solution at the end of phase I serves as a basic feasible solution for phase II. In phase II, the original objective function is introduced and the usual simplex algorithm is used to find an optimal solution. The following are examples of Two Phase Method.
 Two Phase Method: Minimization Example 1
Two Phase Method: Minimization Example 1
Minimize z = -3x1 + x2 - 2x3
subject to
x1 + 3x2 + x3 ≤
5
2x1 – x2 + x3 ≥
2
4x1 + 3x2 - 2x3 = 5
x1, x2, x3 ≥ 0
Solution.
Changing the sense of the optimization
Any linear minimization problem can be viewed as an equivalent linear maximization problem, and vice versa. Specifically:
Minimize![]() cjxj = Maximize
cjxj = Maximize![]() (-
cj)xj
(-
cj)xj
If z is the optimal value of the left-hand expression, then -z is the optimal value of the right-hand expression.
Maximize z = 3x1 – x2 + 2x3
subject to
x1 + 3x2 + x3 ≤
5
2x1 – x2 + x3 ≥
2
4x1 + 3x2 - 2x3 = 5
x1, x2, x3 ≥ 0
Converting inequalities to equalities
x1 + 3x2 + x3 + x4 = 5
2x1 – x2 + x3 – x5 = 2
4x1 + 3x2 - 2x3 = 5
x1, x2, x3, x4, x5 ≥ 0
Where:
x4 is a slack variable
x5 is a surplus variable
Now, if we let x1, x2 and x3 equal to zero in the initial solution, we will have x4 = 5 and x5 = -2, which is not possible because a surplus variable cannot be negative. Therefore, we need artificial variables.
x1 + 3x2 + x3 + x4 = 5
2x1 – x2 + x3 – x5 + A1 = 2
4x1 + 3x2 - 2x3 + A2 = 5
x1, x2, x3, x4, x5, A1, A2 ≥ 0
Where A1 and A2 are artificial variables.
Phase 1 of Two Phase Method
In this phase, we remove the artificial variables and find an initial feasible solution of the original problem. Now the objective function can be expressed as
Maximize 0x1 + 0x2 + 0x3 + 0x4 + 0x5 + (–A1) + (–A2)
subject to
x1 + 3x2 + x3 + x4 = 5
2x1 – x2 + x3 – x5 + A1 = 2
4x1 + 3x2 - 2x3 + A2 = 5
x1, x2, x3, x4, x5, A1, A2 ≥ 0
Initial basic feasible solution
The intial basic feasible solution is obtained by setting
x1 = x2 = x3 = x5 = 0
Then we shall have A1 = 2 , A2 = 5, x4 = 5
Two Phase Method: Table 1
| cj | 0 | 0 | 0 | 0 | 0 | -1 | -1 | ||
|---|---|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x3 | x4 | x5 | A1 | A2 | Solution values b (= XB) |
| 0 | x4 | 1 | 3 | 1 | 1 | 0 | 0 | 0 | 5 |
| -1 | A1 | 2 | -1 | 1 | 0 | -1 | 1 | 0 | 2 |
| -1 | A2 | 4 | 3 | -2 | 0 | 0 | 0 | 1 | 5 |
| zj–cj | -6 | -2 | 1 | 0 | 1 | 0 | 0 |
Key column = x1 column
Minimum (5/1, 2/2, 5/4) = 1
Key row = A1 row
Pivot element = 2
A1 departs and x1 enters.
Table 2
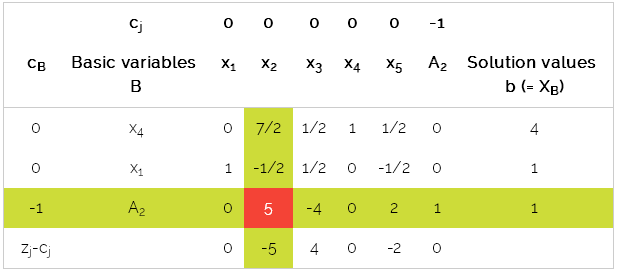
A2 departs and x2 enters.
Here, Phase 1 terminates because both the artificial variables have
been removed from the basis.
Phase 2 of Two Phase Method
The basic feasible solution at the end of Phase 1 computation is used as the initial basic feasible solution of the problem. The original objective function is introduced in Phase 2 computation and the usual simplex procedure is used to solve the problem.
Table 3
| cj | 3 | -1 | 2 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x3 | x4 | x5 | Solution values b (= XB) |
| 0 | x4 | 0 | 0 | 33/10 | 1 | -9/10 | 33/10 |
| 3 | x1 | 1 | 0 | 1/10 | 0 | -3/10 | 11/10 |
| -1 | x2 | 0 | 1 | -4/5 | 0 | 2/5 | 1/5 |
| zj-cj | 0 | 0 | -9/10 | 0 | -13/10 |
Table 4
| cj | 3 | -1 | 2 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x3 | x4 | x5 | Solution values b (= XB) |
| 0 | x4 | 0 | 9/4 | 3/2 | 1 | 0 | 15/4 |
| 3 | x1 | 1 | 3/4 | -1/2 | 0 | 0 | 5/4 |
| 0 | x5 | 0 | 5/2 | -2 | 0 | 1 | 1/2 |
| zj-cj | 0 | 13/4 | -7/2 | 0 | 0 |
![]() Don't be impatient.
The next table is the last table.
Don't be impatient.
The next table is the last table.
Two Phase Method: Final Optimal Table
| cj | 3 | -1 | 2 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x3 | x4 | x5 | Solution values b (= XB) |
| 2 | x3 | 0 | 3/2 | 1 | 2/3 | 0 | 5/2 |
| 3 | x1 | 1 | 3/2 | 0 | 1/3 | 0 | 5/2 |
| 0 | x5 | 0 | 11/2 | 0 | 4/3 | 1 | 11/2 |
| zj-cj | 0 | 17/2 | 0 | 7/3 | 0 |
An optimal policy is x1 = 5/2, x2 = 0, x3 = 5/2. The associated optimal value of the objective function is z = 3 X (5/2) – 0 + 2 X (5/2) = 25/2.



